
blastFoam
blastFoam is a solver for multi-component compressible flow with application to high-explosive detonation, explosive safety and airblast. blastFoam is developed by Synthetik Applied Technologies.
Disclaimer
This offering is not approved or endorsed by OpenCFD Limited, producer and distributor of the OpenFOAM software via www.openfoam.com, and owner of the OPENFOAM and OpenCFD trade marks.
What is blastFoam?
blastFoam is a solver for multi-component compressible flow with application to high-explosive detonation, explosive safety and airblast. The blastFoam solver uses OpenFOAM technology, and is in no way approved or endorsed by OpenCFD Limited, producer and distributor of the OpenFOAM software via www.openfoam.com, and owner of the OPENFOAM and OpenCFD trade marks (see Disclaimer above).
How to use blastFoam
Several validation and tutorial cases are included in the repository, and are documented in the blastFoam User Guide.
Installation
- Install OpenFOAM from source or via binary/package installation from here (blastFoam works with OF version 7).
- Clone the blastFoam repository
git clone https://github.com/synthetik-technologies/blastfoam.git
- Run the ./Allwmake script to compile and install blastFoam
cd blastfoam
./Allwmake
- Test your installation by running the tutorial and validation cases
Questions and Availability
If you find any bugs, please let us know in the issues section of the repository. If you want to get in touch: info@synthetik-technologies.com
blastFoam is also available on the Texas Advanced Computing Center https://www.tacc.utexas.edu (TACC)
Citation
If you use this code for your work or research, please use this citation:
blastFoam: An OpenFOAM Solver for Compressible Multi-Fluid Flow with Application to High-Explosive Detonation. Synthetik Applied Technologies, LLC., 2019.
BiBTex:
@software{blastfoam,
title = {{blastFoam}: A Solver for Compressible Multi-Fluid Flow with Application to High-Explosive Detonation},
url = {https://github.com/synthetik-technologies/blastfoam},
publisher = {Synthetik Applied Technologies, {LLC}.},
date = {2019-10-22}
}
User Guide
To cite the blastFoam User Guide.:
J. Heylmun, P. Vonk, and T. Brewer, “blastFoam User Guide.” Synthetik Applied Technologies, LLC., 30-Oct-2019.
BiBTex:
@misc{heylmun_blastfoamguide_2019,
title = {{blastFoam version 2.0} {User} {Guide} },
url = {https://github.com/synthetik-technologies/blastfoam},
language = {English},
publisher = {Synthetik Applied Technologies, LLC.},
author = {Heylmun, Jeffrey and Vonk, Peter and Brewer, Timothy},
month = oct,
year = {2019}
}
blastFoam Publications:
Journals/Conferences
- T. Brewer, J. Heylmun, and P. Vonk, “Employment of the Open-source Airblast Solver blastFoam to Support the Super Heavy Improvised Explosive Loading Demonstration (SHIELD) Test Program,” presented at the ISIEMS, USA, 2019.
- D. Stephens, P. Vonk, and T. Brewer, “Validation of Open-source Airblast Solver (blastFoam) in an Urban Environment,” presented at the MABS 25, Hague, Netherlands, 2018.
- P. Vonk, “A New OpenFOAM Solver for Compressible Multi-Fluid Flow with Application to High-Explosive Detonation,” presented at the OpenFOAM Users Conference, Cologne, Germany, 2016.
- P. Vonk, T. Brewer, “A New OpenFOAM Solver for Compressible Multi-Fluid Flow with Application to High-Explosive Detonation and Extended Validation,” presented at the OpenFOAM Users Conference, USA, 2016.
Features
blastFoam currently supports the following features:
- An arbitrary number of phases/EOS's
- JLW equation of state with constant, linear, and "Miller" afterburn models
- Multiple example and tutorial cases
- Automatic mesh refinement (AMR)
- Single and multi-point detonation
- High-order (1st, 2nd, 3rd and 4th order in time; 2nd and 3rd order spatial)
- HLLC, AUSM+, Kurganov, Tadmor flux schemes
- Parallel (MPI)
- Compatible with all of OpenFOAM's standard mesh generation, pre- and post-processing utilities
Equations of State
blastFoam includes the following equations of state:
- Jones Wilkens Lee (JWL) (with afterburn)
- Ideal Gas
- Stiffened Gas
- Cochran-Chan
- Tait
- Van der Waals
Verification and Validation
blastFoam has been validated against known solutions to standard gas dynamics problems, and against data from physical tests. Validation cases are included with example/tutorial cases as part of the solver source code.
Validation/Example: Internal Detonation
Reference:
Joachim, Charles E., Gordon W. McMahon, Christo V. Lunderman, and Sharon B. Garner. 1999. “Airblast Effects Research: Small-Scale Experiments and Calculations.” DTIC Document.
Validation against experimental and simulated (CTH) data as reported in Joachim et. al.; see the paper for an explanation of scaling.
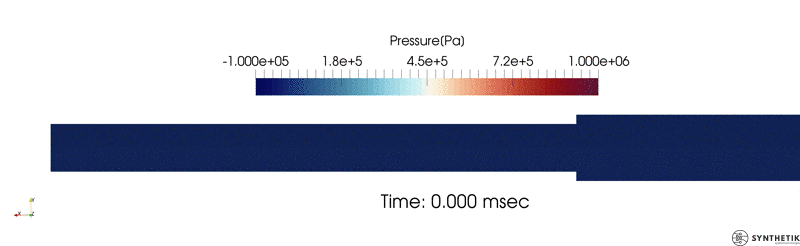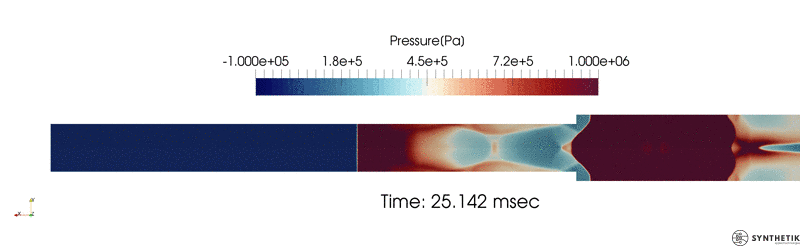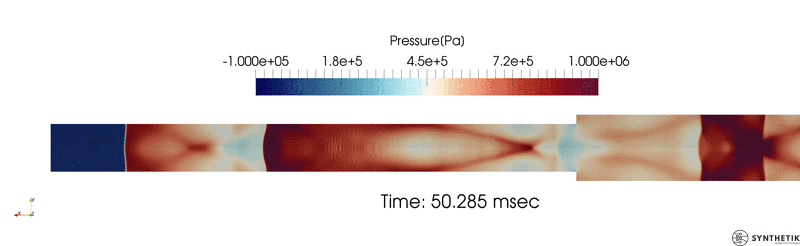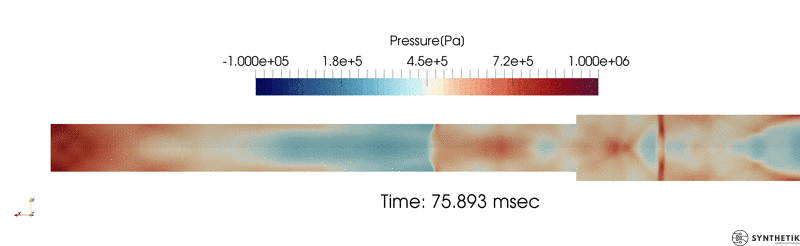
Validation/Example: Blast Loads Behind Vertical Walls
Reference:
M. E. Beyer, “Blast Loads Behind Vertical Walls,” Naval Civil Engineering Laboratory, Port Hueneme, CA, USA, AD-A181 274, 1986.

Validation/Example: Multi-Component Flow Verification
Reference:
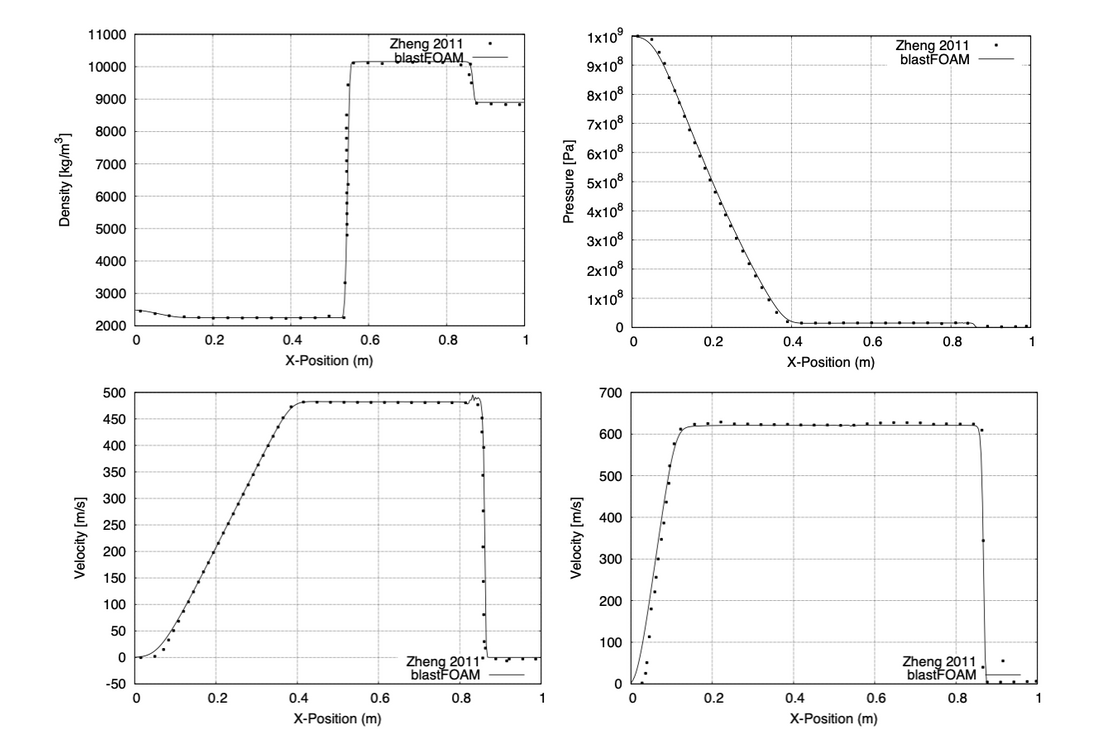
Zheng, H. W., C. Shu, Y. T. Chew, and N. Qin. “A Solution Adaptive Simulation of Compressible Multi-Fluid Flows with General Equation of State.” International Journal for Numerical Methods in Fluids 67, no. 5 (2011): 616–637.
Verification and validation results as compared to those published by Zheng et. al.; HLLC flux shown.
Governing Equations
The evolution of a two phase, compressible, and inviscid mixture can be defined by a set of coupled evolution equations for mass, momentum, and energy.
where is the mixture density, the mixture velocity, the total energy, the pressure, and and are the density and volume fraction of each phase.
The pressure will be defined using a specified equation of state where the mixture internal energy, densities, and volume fraction are used to calculate the total pressure. The equations of state will be used in the Mie-Gruneisen form.
Equations of State
The mixture pressure is defined using the Mie-Gruneisen from using
where
and is dependent on the equation of state.
The speed of sound within a give phase is give by
with
and is again dependent on the equation of state.
Generalized van der Waals gas
For a gas described by the generalized van der Waals equation of state, the pressure is defined as
where , , , and are material parameters. Writing the above equation in M.G. form, we obtain
and
Tait's equation of state
For a material obeying the Tait EOS, the pressure is defined as
where , , and are material properties. In M.G. form, we have
and
Stiffened gas
For a material obeying the stiffened EOS, the pressure is defined as
where and are material properties, and
Jones Wilkins Lee (JWL)
The more complicated JWL EOS is often used to define energetic materials, and has a reference pressure given by
, , , , , and are the material properties. The functions of the EOS are given by
and
is anther material parameter which denotes a reference energy state.
Cochran Chan
The Cochran Chan EOS can be used to describe solid material, and has a reference pressure given by
, , , , , and are the material properties. The functions of the EOS are given by
where again, is a material parameter which denotes a reference energy state.